- Strategies for Finding Training Snapshots for the Hyperreduction Method ECSW in Magnetodynamic Systems. PAMM 22 (1), 2023 mehr… Volltext ( DOI ) Volltext (mediaTUM)
- Model order reduction using hyperreduction methods (DEIM, ECSW) for magnetodynamic FEM problems. Finite Elements in Analysis and Design 209, 2022, 103793 mehr… Volltext ( DOI ) Volltext (mediaTUM)
- Multiphysical Simulation, Model Order Reduction (ECSW) and Experimental Validation of an Active Magnetic Bearing. Actuators 11 (6), 2022, 169 mehr… Volltext ( DOI ) Volltext (mediaTUM)
Model Order Reduction
Many advanced structures, such as compliant mechanisms, Microelectromechanical Systems (MEMS) or wind turbine blades undergo large deflections. Such structures are typically analyzed with Finite Element Simulations. The equations of motion that result from the Finite Element formulation are nonlinear due to the large deflections of the structure. When performing design studies of such structures, these equations must be solved several times that makes the study take a lot of computation time. The goal of this project is to develop model reduction methods that are able to reduce computation time and make design studies feasible.
Hyperreduction for Non-linear Systems
Two steps are necessary to reduce a non-linear finite element model:
- Projection
- Hyperreduction
The chair of applied mechanics develops methods for these two steps with the focus on cheap computations.
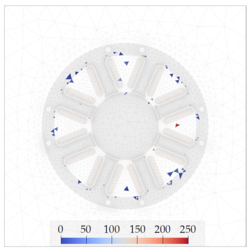
MOR for Magnetodynamic Systems
Electromechanic systems are omnipresent. The range is from small devices as headphones to wind turbine generators. To allow an efficient operation of these devices, the magnetic field needs to be strong enough to max out the ferromagnetic material. This leads to non-linear effects arising from the saturation of the ferromagnetic material. The need for model order reduction becomes clear by considering the mesh size needed to correctly represent the Eddy-current distribution due to the skin effect.
Here you can find a video.
Model order reduction has in general two major fields of applications. On the one hand the development phase of a product, where faster simulations allow for more complex optimisation routines that end up in better products. On the other hand during the operation of complex systems, where slim models are needed to perform predictions on the health status of the machine using very limited edge computing performance.
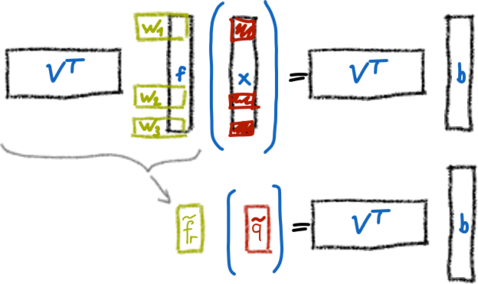
Reduction methods based on projection of the problem in a subspace perform well only for linear problems that can be projected cost-effectively in a subspace. The focus here is on methods that use a second reduction, the so-called hyperreduction, of the non-linear internal forces to speed the calculation up. Two methods used in structural mechanics are transformed for magnetodynamic systems.
The first approach is called the Discrete Empirical Interpolation method (DEIM) and tries to approximate the full non-linear internal forces by expanding the force of selected dofs via a dedicated basis.
The second method is the Energy Conserving Sampling and Weighting Method (ECSW) that weights selected elements such that the internal forces produce the same virtual work as the non-reduced system.
Both methods gain their time reduction from the idea to reduce the number of elements called for the computation of the non-linear internal force term.
Johannes Maierhofer, M.Sc.
Approaches for dealing with design parameters
We consider three main approaches to apply model reduction for design studies:
- Global Approach: This approach uses one single reduced order model that is used for the full parameter space of interest.
- Updating Approach: This approach starts at one design point and updates the reduced order model when parameter values move away from the initial design point.
- Interpolation Approach: This approach computes reduced order models at several sampling points and interpolates between these models to gain reduced models at new design points.
Current Projects
of local visco-elastic damping layer placements for design of calm, smart and smooth structures
Numerical and experimental optimization of local visco-elastic damping layer placements for design of calm, smart and smooth structures
A key aspect to build calm structures is the application of damping layers. They are cheap and easy to install. But their disadvantage is that they add extra weight to the structure. For this reason, one would like to minimize the amount of added material and optimize the location of their application.
Numerical simulations, that predict the behavior of structures with damping layers, are often modeled with the Rayleigh damping assumption, which is simple but cannot adequately represent actual behavior. Damping models that are able to represent viscoelastic behavior can give more realistic results. However, their main drawback is that they drastically increase computation time which make optimization and design studies infeasible.
The main goal of this project is to develop model reduction methods for models that contain viscoelastic materials. This can help to reduce computation time to make optimization and fast design studies for structures with applied viscoelastic damping layers possible.
Previous members
- Dipl.-Ing. Johannes Rutzmoser
- Christian H. Meyer, M.Sc.
- Johannes Maierhofer, M.Sc.