Optische Methoden in der experimentellen Dynamik
In der experimentellen Strukturdynamik müssen Bewegungen von Strukturen gemessen werden, um sie zu analysieren. Dabei spielt es theoretisch keine Rolle, ob Verschiebungen, Geschwindigkeiten oder Beschleunigungen erfasst werden, was eine Vielzahl von möglichen Messstrategien bedeutet.
Während die meisten Messungen im Rahmen der experimentellen Strukturdynamik mit piezoelektrischen Beschleunigungssensoren durchgeführt werden, die an der untersuchten Struktur befestigt werden, gibt es auch berührungslose Methoden, die Messungen an sonst schwer zugänglichen Stellen ermöglichen und die Dynamik des zu messenden Objekts nicht beeinflussen.
Am Lehrstuhl für Angewandte Mechanik erforschen wir zwei dieser Methoden im Detail und arbeiten an der Erweiterung ihrer Einsatzmöglichkeiten.
Laser-Doppler-Vibrometrie
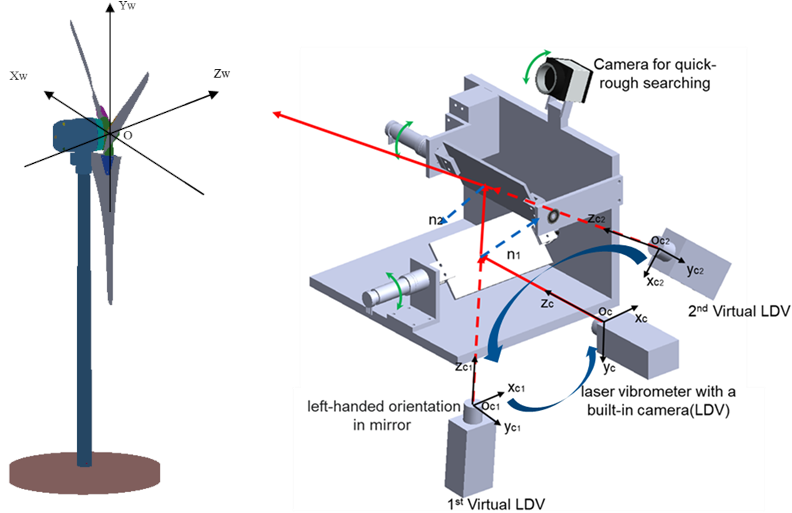
Ein Laser-Doppler-Vibrometer (LDV) nutzt das Prinzip des Doppler-Effekts, um die Eigenschaften von mechanischen Schwingungen oder transienten Bewegungsvorgängen zu erfassen. LDVs ermöglichen eine äußerst präzise Messung von Oberflächengeschwindigkeiten, die aber auf eine Richtung (entlang des Laserstrahls) und einen Punkt beschränkt ist. An unserem Lehrstuhl wird ein Prototyp eines automatisch nachgeführten Scanning Laser-Doppler-Vibrometers (SLDV) entwickelt. Dieses SLDV besteht aus einem Laser-Doppler-Vibrometer mit zwei zusätzlichen orthogonal ausgerichteten Spiegeln und einem Bildverarbeitungssystem.
Wir entwickeln eine neue Strategie zur genauen Verfolgung von bewegten Objekten und Modellierung ihrer Geschwindigkeit auf der Grundlage der eingebauten Kamera des LDV. Außerdem werden Experimente an einem Windrad durchgeführt, um die Funktionsfähigkeit des SLDV-Systems zu überprüfen.
Messung mit Hochgeschwindigkeitskameras
Eine andere Strategie zur Messung von Schwingungen einer Struktur besteht darin, ein Video von ihr aufzunehmen und daraus Verschiebungen zu bestimmen. Dazu wird auf der Oberfläche in der Regel ein Schwarz-Weiß-Muster befestigt, um den Kontrast zu erhöhen und genauere Messungen zu ermöglichen.
Hochgeschwindigkeitskameras bieten große Vorteile, haben aber auch gravierende Nachteile.
Im Vergleich zu Beschleunigungssensoren oder LDV ist das Rauschverhalten aufgrund des geringeren Dynamikbereichs von Bildsensoren wesentlich schlechter. Außerdem erzeugen Kamerasensoren riesige Datenmengen, nur kleine Teile effektiv genutzt werden, da nur Pixel in der Nähe kontrastreicher Kanten zur Erkennung von Verschiebungen verwendet werden. Aufgrund des begrenzten und sehr teuren schnellen Speichers der Kamera begrenzt die Datenmenge die maximal mögliche Dauer der Messungen direkt ein.
Während diese Nachteile viele Probleme bei der Arbeit mit den gemessenen Verschiebungen mit sich bringen, sind die Vorteile der kamerabasierten Messungen die Mühe wert: Abgesehen davon, dass die Messungen berührungslos sind, bietet eine Kameramessung die Möglichkeit, eine beispiellose Menge an Punkten gleichzeitig zum messen.
Wir untersuchen, wie 3D-Messungen mit Spiegeln durchgeführt werden können, und nutzen die Ergebnisse zur Durchführung von Modalanalysen.

Operational Modalanalyse
Wir konzentrieren uns nicht nur auf die Messtechniken, sondern arbeiten auch an deren Anwendung im Rahmen der Modalanalyse. Die Modalanalyse beschreibt den Prozess der Ermittlung sogenannter Modalparameter einer Struktur wie Eigenfrequenzen und Eingenschwingformen. Diese Parameter sind in fast allen technischen Bereichen sehr wichtig, und ihre Bestimmung kann Ingenieuren Einblicke in die strukturelle Integrität eines bestimmten Systems geben oder in frühen Entwicklungsphasen helfen, wenn Prototypen analysiert werden.
Die operational Modalanalyse (OMA) beschreibt eine spezielle Variante der Modalanalyse, bei der es ausreicht, die Schwingungen einer Struktur zu messen, ohne den Krafteintrag, der zu den Schwingungen geführt hat, genau zu kennen. OMA ist besonders nützlich für sehr große Strukturen wie Gebäude, Windkraftanlagen, die nicht kontrolliert angeregt werden können, sowie alle Strukturen, die im Betriebszustand Belastungen ausgesetzt sind, die in einer Laborumgebung nicht entsprechend realistisch nachgebildet werden können.
Eine Einschränkung der Standard-OMA-Ansätze besteht darin, dass das System als linear zeitinvariant (LTI) angenommen wird, was z.B. bei Windkraftanlagen mit rotierenden Flügeln nicht der Fall ist. Daher arbeiten wir an einem verbesserten OMA-Ansatz für linear-zeitperiodische (LTP) Systeme.
Kontakt
- Dong Li, M.Sc.
- Max Gille, M.Sc.