In experimental structural dynamics, to assess the movements of structures, these movements must be somehow measured. In theory, it doesn’t matter whether displacements, velocities or accelerations are recorded. This fact results in a variety of possible measurement strategies.
While most measurements in the context of experimental structural dynamics are conducted using piezo-electric accelerometers that are fixed on the investigated structure’s surface, there also exist contact-less methods which enable measurements at otherwise hard-to-reach points and don’t influence the object’s dynamics.
At the Chair of Applied Mechanics, we are researching two of those methods in detail and work on expanding their possible applications.
Laser-Doppler-Vibrometry
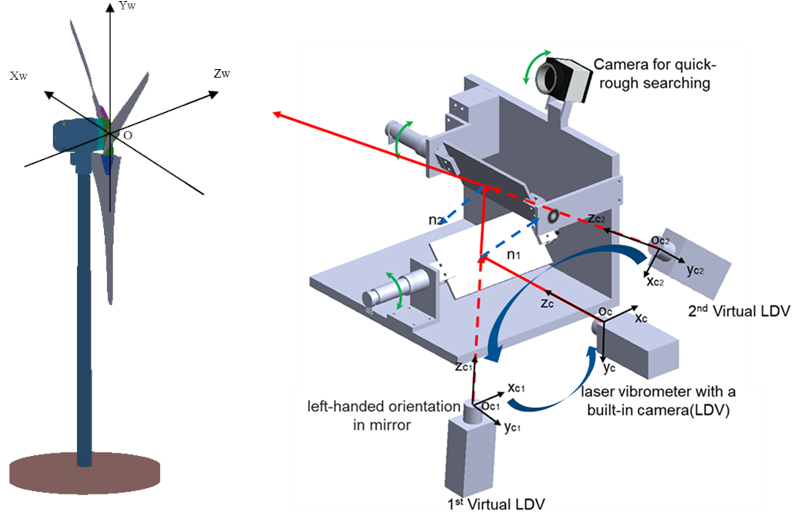
The laser Doppler vibrometer (LDV) uses the principle of the Doppler effect to acquire the characteristics of mechanical vibrations or transient motion processes. LDV enables an extremely precise measurement of surface velocities but it’s limited to just one direction (along the laser beam) and one point at a time. A prototype of a self-tracking scanning laser Doppler vibrometer (SLDV) is developed in our chair. The self-tracking SLDV is composed of a laser Doppler vibrometer with the addition of two orthogonally aligned mirrors and an image-processing system.
A new strategy for accurate tracking and modeling of the measured velocity based on the built-in camera of the LDV is presented. Furthermore, an experiment on the wind turbine is established to validate the effectiveness of the self-tracking LDV system.
High Speed Imaging
Another strategy for assessing a structure’s vibrations is by simply taking a video of it and extracting the observable displacements. Typically, the surface is therefore prepared with a black/white pattern to higher the contrast and enable more sensitive measurements.
High Speed Cameras (HSC) offer great advantages, but also suffer from severe drawbacks.
Compared to accelerometers or LDV, the signal to noise ratio is far worse due to the lower dynamic range of image sensors compared to traditional measurement hardware. Also, camera sensors produce huge amounts of data, and the least of it is effectively used in the end as only pixels near high-contrast edges are used to identify displacements. Due to limited and very expensive fast memory on the camera, the amount of data directly limits the maximum possible duration of measurements.
While those drawbacks bring plenty of problems when working with the measured displacements, the advantage of camera-based measurements are worth the trouble: In addition to the measurements being contact-less and thus non-intrusive, a camera measurement offers an unparalleled spatial resolution with possibly hundreds of points analyzed at once.
We explore ways to achieve 3D measurements with mirrors and use the results to perform operational modal analysis.

Operational Modal Analysis
We do not focus on the measurement techniques only, but also work on their application in the context of modal analysis. Modal analysis describes the process of finding the so-called modal parameters of a structure, among them eigenfrequencies and mode shapes (shapes in which a structure vibrates uniformly at a given eigenfrequency). These parameters are very important measures in almost every engineering domain and their analysis can give engineers meaningful insights into the structural integrity of a given system or help in early development phases when prototypes are analyzed.
Operational modal analysis (OMA) describes a special variant of modal analysis for which it sufficient to measure a structure’s vibrations without exactly knowing the force input that led to the vibration in the first place. This technique is especially useful for very large structures such as buildings, wind turbines that cannot be solely excited in a controlled manner, and any structure in operation that undergoes loads that cannot be realistically excited accordingly in a lab environment.
One limitation of standard OMA approaches is that the system is assumed to be linear time invariant (LTI), which is not the case for wind turbines with rotating blades. For this case, we work on an improved OMA approach for linear time-periodic (LTP) systems.
- Dong Li, M.Sc.
- Max Gille, M.Sc.